What is a Trie
A lot of you will know a binary tree. You have a root node and depending if the value is greater than the root or node it goes left (if it is less) or right of the root (if it is greater). Every node (including the root node) can only contain at most 2 children. If we want to add a new item to our tree we have to add a new level with the rules described above.
The Trie is not far from that. Instead of having at most 2 children we can have k children (so an arbitrary number). The idea is that we add words by their individual character. If two words have the same prefix (so the beginning of the word) they share this exact same prefix in our tree, Let's have a look at the following animation to make it a bit more visible. We add the following three words: Tree, Trie, Tetris
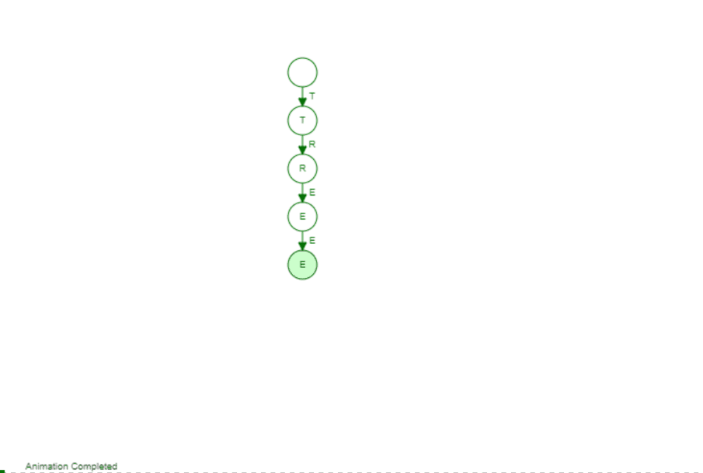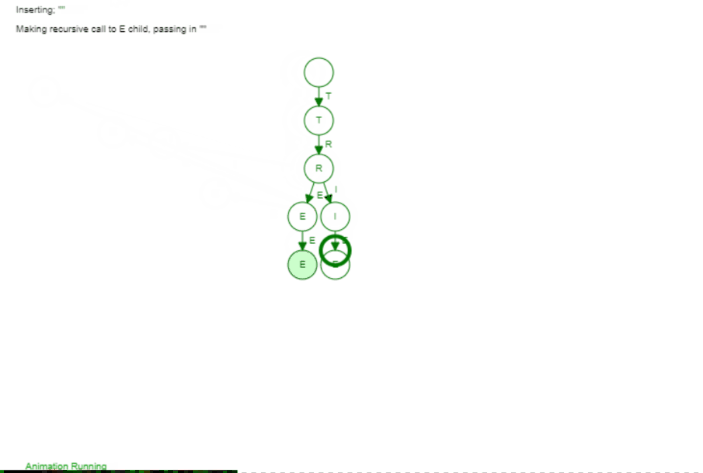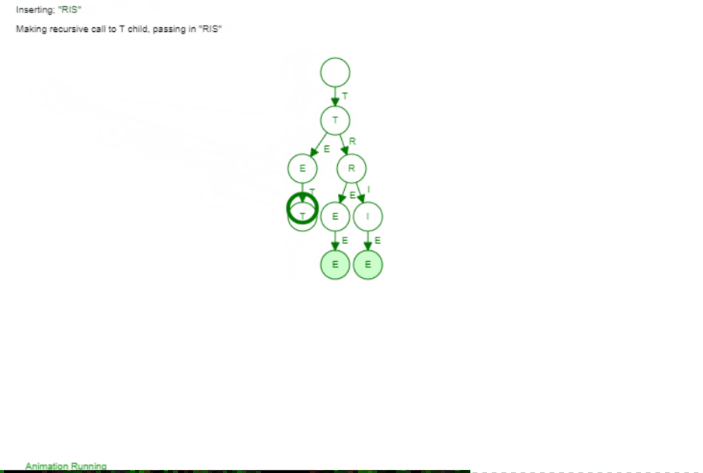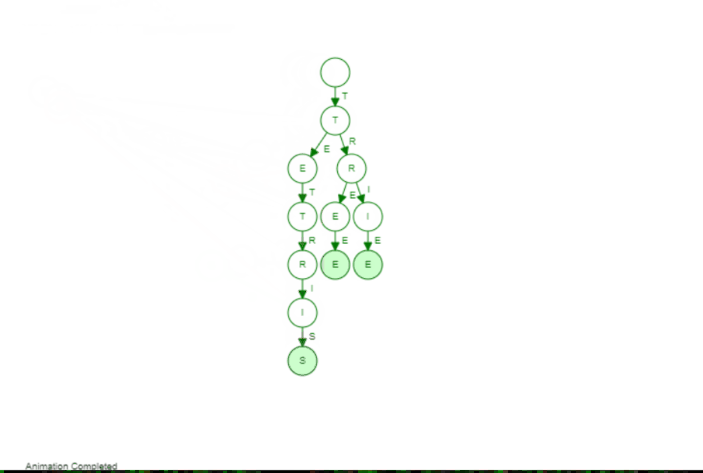
The first word Tree is just a "line". But we can see as soon as we add the second word Trie we branch of after Tr. That makes sense as Tree and Trie share the prefix Tr. When we add Tetris we branch of after the T because only the T is the common prefix between all those words. If we would add a word like Banana we would have no common prefix at all and would branch off of the root node (the empty element on top).
Before we dive into code I want to highlight why this is a nice data structure for autocompletion. Let's assume in our example the user types in "Tr". If we go down our Trie we know that Tree and Trie share this prefix. Tada we got our word. Also looking for a specific word is easy as we only have to follow the branches of our Trie and check whether or not we find a leaf.
Time and space complexity
Now a word about time and space complexity. Adding a new word can take up to the whole amount of the word we want to add. But that is the worst case. Just remember our banana example from above. we only had words with T therefore banana would take additional 7 characters on our Trie. But if we would add the word Tea, this would only take the additional a.
- Space Complexity Worst-Case: O(n)
- Space Complexity Average-Case: O(n)
Where the Trie shines is in its time complexity. For search, insert, delete and finding words based on a given prefix it always takes O(n) time. n here means the word we want to insert, search or delete. And that is in direct contrast to an HashSet which we will later check.
The following chapter will show how to build your own Trie.
Adding an item
Lets begin create our Trie class.
/// This represents the Trie. More specific this would be a TrieNode but we keep it simple.
/// The user would hold the "root" node
public class Trie
{
// if we have a leaf then we know that node is the end of some word
private bool isLeaf;
// We can have k children. The key of the dictionary is "our" current character
private IDictionary<char, Trie> Children { get; set; } = new Dictionary<char, Trie>();
}
I will comment the code as much as possible to guide you what is happening.
public void Add(ReadOnlySpan<char> word)
{
var current = Children;
// We want to go through every element of our word
for (var i = 0; i < word.Length; i++)
{
// For every character we check whether or node we already have this in our Trie
var node = CreateOrGetNode(word[i], current);
// Set the current node to the one returned so in the next iteration of the for loop we can check against this letter
current = node.Children;
// If we are at the last character (so our word is completely integrated) mark this node as leaf
if (i == word.Length - 1)
{
node.isLeaf = true;
}
}
}
private static Trie CreateOrGetNode(char currentCharacter, IDictionary<char, Trie> children)
{
Trie trie;
// If the character we are iterating through already exists then we have a shared prefix
// Imagine we added Tree already and want to add "Trie" now.
// Now we want to add the "T" of "Trie" then this if would evaluate to true as this is already in our data structure
if (children.ContainsKey(currentCharacter))
{
trie = children[currentCharacter];
}
// If not we create a new branch with the current letter
else
{
trie = new Trie();
children.Add(currentCharacter, trie);
}
return trie;
}
Find
public bool Find(ReadOnlySpan<char> word)
{
// Check just if the word is empty. If so return always false. You could also always return true.
if (word.IsEmpty)
{
return false;
}
// Find the node in our trie which has the word
var node = FindNode(word);
// If the node is null that means FindNode didn't find the word
// But we also have to check whether or not the node is a leaf
// Imagine we add the word "Hello" to our Trie. If we then afterwards want to Find "hel" this should return false.
// "hel" is only a common prefix but we never added the word "hel" itself
return node != null && node.isLeaf;
}
private Trie FindNode(ReadOnlySpan<char> word)
{
var children = Children;
Trie currentTrie = null;
// we just go through all the children until we are done with all the characters of our word
foreach (var character in word)
{
// If we found the current character we save the node and continue
if (children.ContainsKey(character))
{
currentTrie = children[character];
children = currentTrie.Children;
}
// if the character is not present we know we don't have this word
else
{
return null;
}
}
return currentTrie;
}
StartsWith
Well this one is a simplification of the last one. We just want to know if we have this string present in our Trie.
public bool StartsWith(ReadOnlySpan<char> word)
{
if (word.IsEmpty)
{
return false;
}
// Here is the difference. We don't care if it isn't a leave.
return FindNode(word) != null;
}
GetWordsWithPrefix
Now this one we can leverage for auto completion. Imagine we have the words "Hello", "Tea", "Home" and "Herbs" in our Trie. A call to StartsWith("He") should return "Hello" and "Herbs".
public IEnumerable<string> GetWordsWithPrefix(string prefix)
{
// Find the node (like StartsWith)
var node = FindNode(prefix);
if (node == null)
{
// If we can't find the node we are done. We found all the words starting with the prefix (or none)
yield break;
}
// We return every word we found given by the prefix
// We just have to go down all possible branches from the found node... so basically all the children
// That is what Collect does
foreach (var word in Collect(node, prefix.ToList()))
{
yield return word;
}
static IEnumerable<string> Collect(Trie node, List<char> prefix)
{
// If we don't have any further children, we are done, we are at the end!
if (node.Children.Count == 0)
{
yield return new string(prefix.ToArray());
}
// Go through every child
foreach (var child in node.Children)
{
// We collect recursively. Because also our children will have children. So what we are doing here is breadth first
prefix.Add(child.Key);
foreach (var t in Collect(child.Value, prefix))
{
yield return t;
}
// We found something therefore we remove the last element and go to the next word
prefix.RemoveAt(prefix.Count - 1);
}
}
}
At the end under Resources you will find all the code again if you want to have a look at the full picture.
Performance
I used the following test setup: I took the most common 1000 wordsfrom here of the English language and added those once in an HashSet and once to our newly defined Trie. Afterwards I compared the time it took for both a) to find a single word and b) find all words which share a given prefix. Here is the test setup:
public class TrieVsHashSet
{
private readonly HashSet<string> _hashSet = new();
private readonly Trie _trie = new();
[GlobalSetup]
public void Setup()
{
var wordsToAdd = File.ReadAllLines("1000words.txt");
foreach (var word in wordsToAdd)
{
_hashSet.Add(word);
_trie.Add(word);
}
}
[Benchmark]
public IList<string> FindAllInHashSet() => _hashSet.Where(h => h.StartsWith("Hel")).ToList();
[Benchmark]
public IList<string> FindAllInTrie() => _trie.GetWordsWithPrefix("Hel").ToList();
[Benchmark]
public bool FindOneInHashSet() => _hashSet.Any(h => h == "happy");
[Benchmark]
public bool FindOneInTrie() => _trie.Find("happy");
}
And here are the results:
BenchmarkDotNet=v0.13.1, OS=Windows 10.0.19043.1586 (21H1/May2021Update)
Intel Core i7-7820HQ CPU 2.90GHz (Kaby Lake), 1 CPU, 8 logical and 4 physical cores
.NET SDK=6.0.201
[Host] : .NET 6.0.3 (6.0.322.12309), X64 RyuJIT
DefaultJob : .NET 6.0.3 (6.0.322.12309), X64 RyuJIT
| Method | Mean | Error | StdDev | Gen 0 | Allocated |
|----------------- |-------------:|-----------:|-----------:|-------:|----------:|
| FindAllInHashSet | 34,846.74 ns | 261.200 ns | 231.547 ns | - | 128 B |
| FindAllInTrie | 45.53 ns | 0.585 ns | 0.547 ns | 0.0229 | 96 B |
| FindOneInHashSet | 5,285.91 ns | 102.328 ns | 109.490 ns | 0.0076 | 40 B |
| FindOneInTrie | 85.50 ns | 0.501 ns | 0.444 ns | - | - |
There is no comparison. The HashSet is 100x slower than our Trie. And the code we have is not optimized very well. The only optimization I took is using ReadOnlySpan<char> instead of strings, but we could do even further if we want to. Of course one part of the equation I didn't measure: Add.
Here the HashSet would clearly win. And this paints also our scenario where we would use a Trie. We don't have to rebuild the Trie (or add words) very often but use something like Find or StartsWith often.
Why is the Trie so much faster? If you have a look at the animation on top of the article you can see that we only have to traverse all the individual characters through the Trie to find a word. If we have a word of length 5, we only have to do 5 steps. In a HashSet that is not the case. The time complexity here is log(n) but n is the total amount of entries we have in our hash set and not the length of the word we are looking for.
Here the visualization of finding the word "Trie":
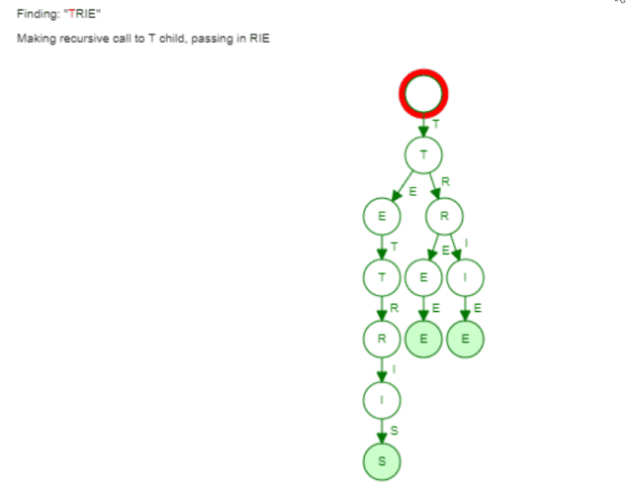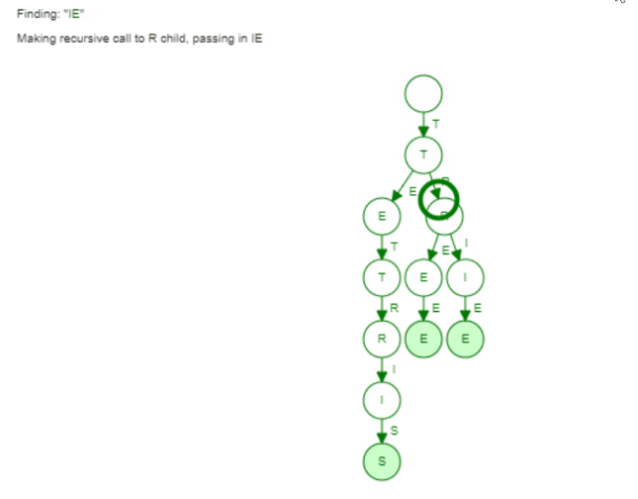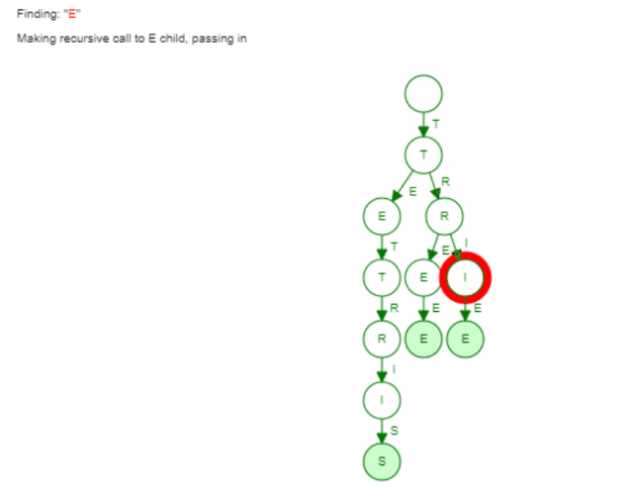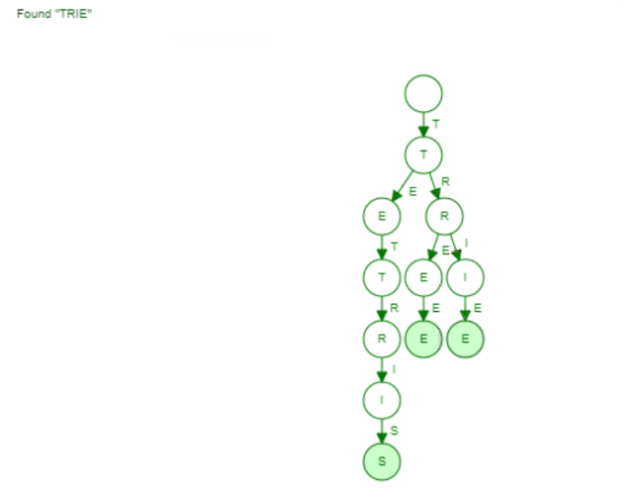
Now the same holds true for finding words with a given prefix. We saw earlier how the collect phase is implemented in our Trie. We only did a Breadth First Search to find all words with this given prefix. Again the hash set can't leverage such information. It has to go through all the buckets to find all words.
Typeahead component in Blazor
We can use our newly created Trie to built a fast typeahead input component. I will post the code and inline all the necessary code section for you to better understand:
@using LinkDotNet.Blog.Web.Features.Components.Typeahead
@* We are using Bootstrap 5 example here. I want my input and the suggestion directly under each other*@
<div class="row">
@*
Every time the user inputs a text we update our suggestion
You could also add debouncing and stuff here
*@
<input @oninput="UpdateAutoCompletion" value="@content"/>
@* Only show suggestions if we have at least one *@
@if (similarWords.Any())
{
@*
Not super sexy but it does what we want. We are using a select element
which shows all the words and we can change/click on it so that the
input element will change
*@
<select size="@AutoCompleteCount" @onchange="UseSelectedWord">
@foreach (var similarWord in similarWords)
{
<option value="@similarWord">@similarWord</option>
}
</select>
}
</div>
@code {
// Let the parent tell which words we have to "index"
[Parameter] public IEnumerable<string> AllWords { get; set; }
// The maximum amount of suggestion we will give
[Parameter] public int AutoCompleteCount { get; set; } = 10;
private readonly Trie trie = new();
private string content = string.Empty;
private List<string> similarWords = new();
// Create the Trie once
// You could also use OnParameterSet and re-create the trie when the parameters change
protected override void OnInitialized()
{
// Lets order the words alphabetically - so it is easier for the user to select her/his word
foreach (var word in AllWords.OrderBy(w => w))
{
trie.Add(word);
}
}
private void UpdateAutoCompletion(ChangeEventArgs inputEventArgs)
{
content = inputEventArgs.Value.ToString();
// Get all words from our Trie which share the prefix (at most AutoCompleteCount)
similarWords = trie.GetWordsWithPrefix(content).Take(AutoCompleteCount).ToList();
}
private void UseSelectedWord(ChangeEventArgs obj)
{
content = obj.Value.ToString();
similarWords.Clear();
}
}
Now only the calling component is missing:
@page "/"
<PageTitle>Index</PageTitle>
<h1>Enter a word (start with captial letter)</h1>
<div class="col-2 ms-5">
<InputTypeAHead AllWords="_words" AutoCompleteCount="5"></InputTypeAHead>
</div>
@code {
private readonly string[] _words =
{
"Cat", "Car", "Dog", "Day", "Hamster", "School", "Sand", "Tea", "Water",
"Cold", "Weather", "Blazor", "Dotnet", "CSharp", "Steven", "Giesel", "Example", "Blog", "Stamp", "Stencil"
};
}
The final result should something like that:
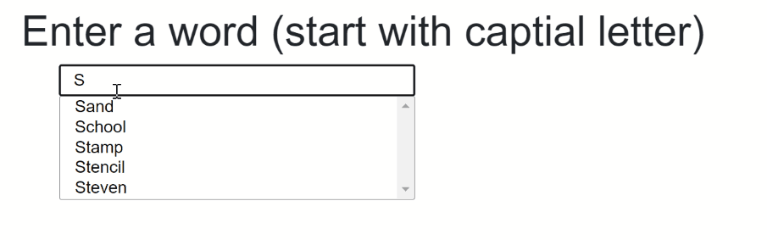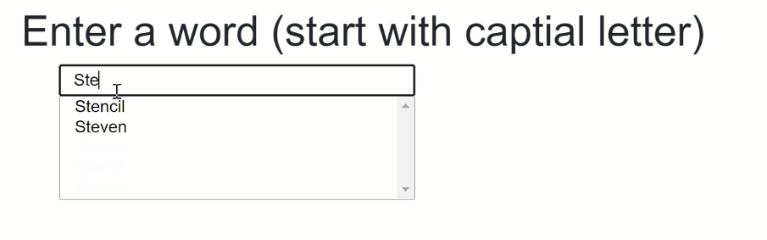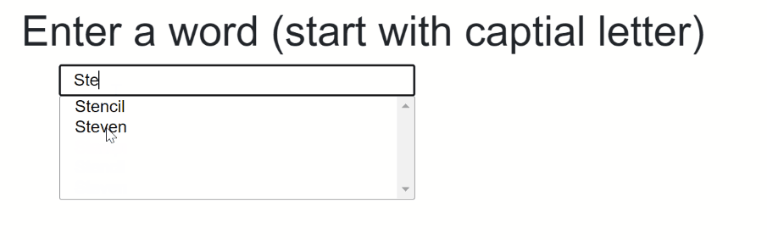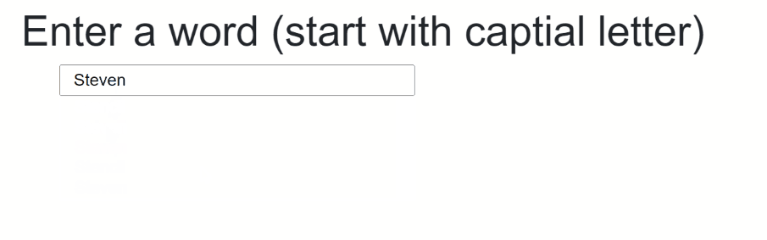
The source code to that can be found here
Limitations
- The biggest issue with this implementation is that the autocomplete only works on single words. We could add "Hello World" to the Trie but the Trie would think it is one word. So typing the prefix "Wo" will not return "World" and typing "Hel" will only return the whole thing "Hello World".
- In its current state "Cat" and "cat" are two different things. The Trie is case sensitive. You can make it easily case insensitiv if you want. I also put down my whole repository with a lot of string algortihms in the Resource section, but here you go if you want to see the implementation which is case insensitive.
Resources
- Trie in C# - A bunch of string algorithms
- Trie in TypeScript - A bunch of string algorithms
- Visualization of Tries
- Source code for the InputTypeAHead can be found here
- Majority of my blog post examples can be found here


