Using SSE in C# on the example of the sum of a list

First of all: What do we want to achieve? That is very easy. We want to leverage our hardware to the fullest. If our CPU has some features we want to use them with C# and now the good news: We can do this!

SSE

SSE are extra instructions in your CPU which enables you to perform a new set of instructions. If you want to know more in great detail here you go.

To give you a general overview what SIMD means have a look at the following picture:

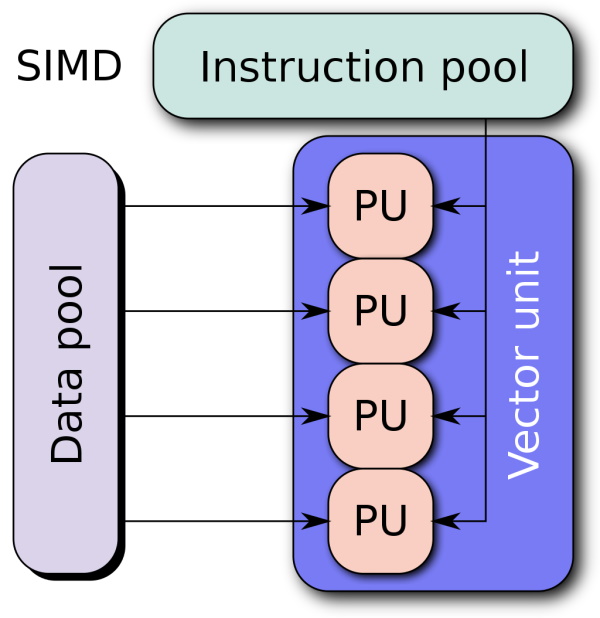
For short it is enough to know that you have one instruction like + (addition) which you can perform on multiple data at the same time. If you want to know more SIMD I already wrote a blog post about ILGPU and the power of SIMD.

C# offers us this API directly via System.Runtime.Intrinsics.X86.Sse2.X64 and indirectly via classes like System.Numerics.Vectors.dll. Of course Vector is the example par excellence. Just thing of adding two vectors. Every date is independent which is the perfect condition for parallelism.

Before we dive into code: I small property Vector.IsHardwareAccelerated will tell you if SSE is enabled in your processor or not. If you are using a Raspberry PI you are out of luck, they do not support SSE. So .NET will fallback to the conventional way of doing things.

Test-Setup

Before we dive into SIMD and how to use it, we want to have some baselines. The obvious candidate is, we are using native for-llop and do the sum on our own:

[Benchmark(Baseline = true)]
public int GetSumNaive()
{
    var result = 0;
    for (var index = 0; index < Numbers.Length; index++)
    {
        var i = Numbers[index];
        result += i;
    }

    return result;
}

I explicitly used a for loop instead of foreach as this feels more natural, plus it is faster.

The next two options are LINQ:

[Benchmark]
public int SumLINQ() => Numbers.Sum();

[Benchmark]
public int SumPLINQ() => Numbers.AsParallel().Sum();

Now to the SIMD version of that all. I commented the code to give you an idea what is going on here:

[Benchmark]
public int SIMDVectors()
{
    // This depends on your hardware
    // It basically says on how many entries can we performance this single operation
    // aka how big is "multiple"
    var vectorSize = Vector<int>.Count;
    var accVector = Vector<int>.Zero;

    // We are tiling the original list by the hardware vector size
    for (var i = 0; i <= Numbers.Length - vectorSize; i += vectorSize)
    {
        var v = new Vector<int>(Numbers, i);
        accVector = Vector.Add(accVector, v);
    }

    // Scalar-Product of our vector against the Unit vector is its sum
    var result = Vector.Dot(accVector, Vector<int>.One);
    return result;
}

The link to this example and all examples in general can be found at the end of the blog post. If we work in a SIMD style we have to wrap our head around the fact that we have to divide and conquer our problems into smaller sub-problems which can be solved independently.

Now without further ado lets show us the results:

|      Method |        Mean |      Error |     StdDev | Ratio | RatioSD |
|------------ |------------:|-----------:|-----------:|------:|--------:|
| GetSumNaive |   313.52 ns |   5.928 ns |   5.545 ns |  1.00 |    0.00 |
|     SumLINQ | 2,630.16 ns |  51.568 ns |  95.585 ns |  8.60 |    0.46 |
|    SumPLINQ | 7,854.96 ns | 145.591 ns | 189.309 ns | 25.16 |    0.93 |
| SIMDVectors |    81.13 ns |   1.661 ns |   3.200 ns |  0.26 |    0.01 |

• I guess to our baseline we don't have to say much.
• The Sum function is slower than our native function. Mainly due to the overhead of foreach and all what comes with it (callvirt, GetEnumerator, ...)
• Our PLINQ is even slower? Well more to that in a second
• SIMD is way ahead. Mainly because this would be one example how to use SIMD/SSE in general. So this is a cherry case 😉

Why is PLINQ so slow? The answer is simple: PLINQ has to detect on its own how to partition the whole thing. Plus it has to find out how the data is related to each other. Which partition is independent etc. Bottom line: Without hints PLINQ falls off.

Conclusion

You might not use SSE/SIMD every day, but if you every come across such stuff you will be glad to hear that such stuff exists.

Resources

• Example-Code of this blog post on Github
• All examples of my blog in general on Github