In this small blog post we will have a look at how HTTPS works. Well, we will look how the cryptographic part works a bit more in detail.
The focus is on the Diffie Hellman Key algorithm, an asymmetric key exchange. We will see what an asymmetric and a symmetric key exchange is.
Motivation
What we want is easy, Alice and Bob want to communicate in a private fashion over a public channel. Public channel means everybody can listen to their conversion (in our case Tom).
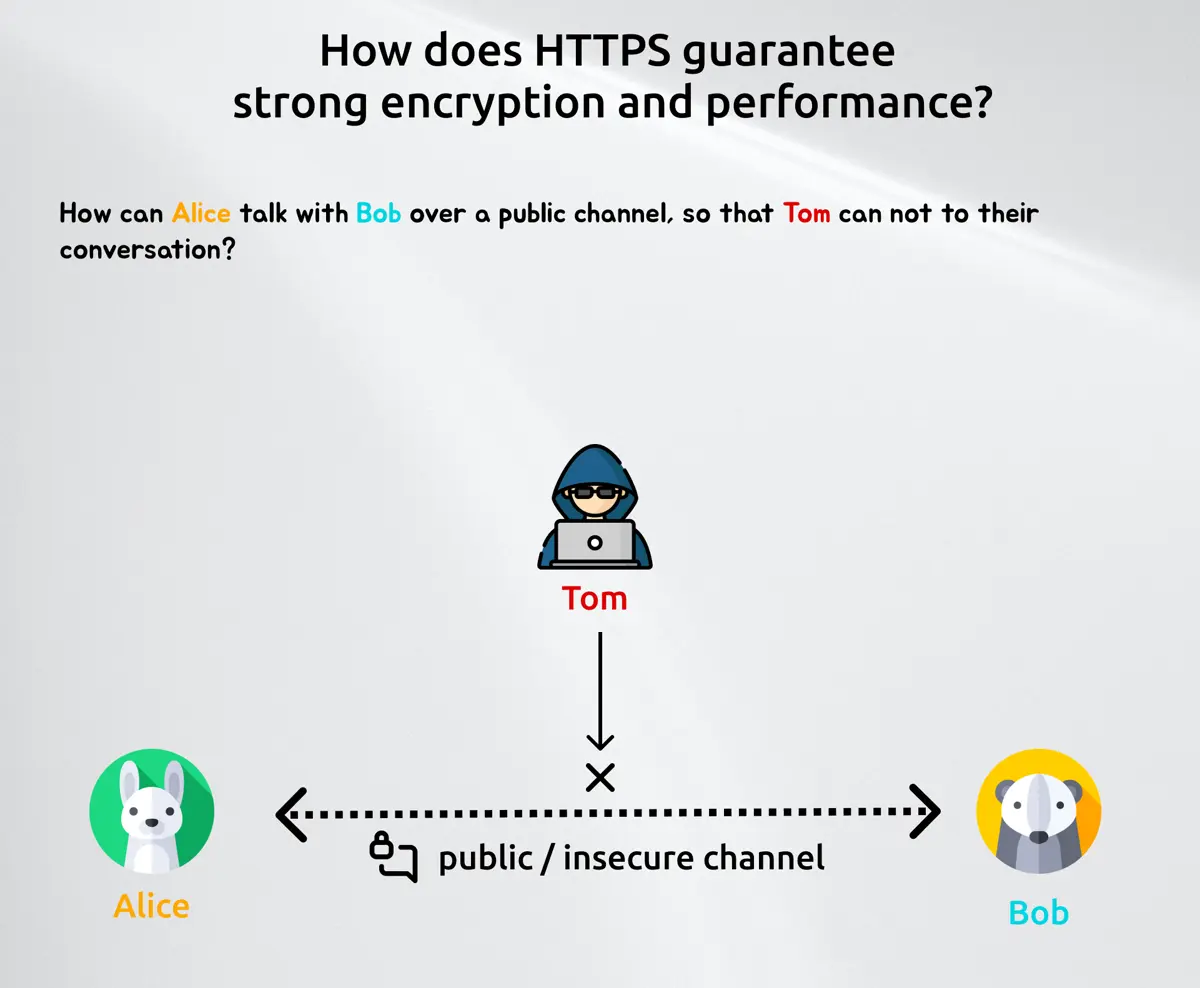
So to make that work we have to find a way to encrypt the messages between those two. Encryption means we need a function which takes a raw and readable input and transforms this into an output, which can only be understood by well-defined actors. One way of making this work is to share a secret beforehand. As Alice and Bob never met in real life, they can't do that so they have to find a way to share or create a secret on the fly. And that is where the Diffie Hellman key exchange comes into play.

What you saw is an asymmetric key exchange. This means that every party always deals with two kind of keys: A public key which is use to decrypt the message and a private key which is used to encrypt a message. A symmetric key exchange only has one single key, which is used for both actions. The advantage of asymmetric encryption is, that it's generally safer but takes more bandwidth and more performance. A symmetric one is faster, but if you get into the possession of said key, than you can decrypt and encrypt every message. We will later see how they play together. Let's first have a small math example how does this public exchange work with private and public key so that Tom can't read Alice or Bob's messages.
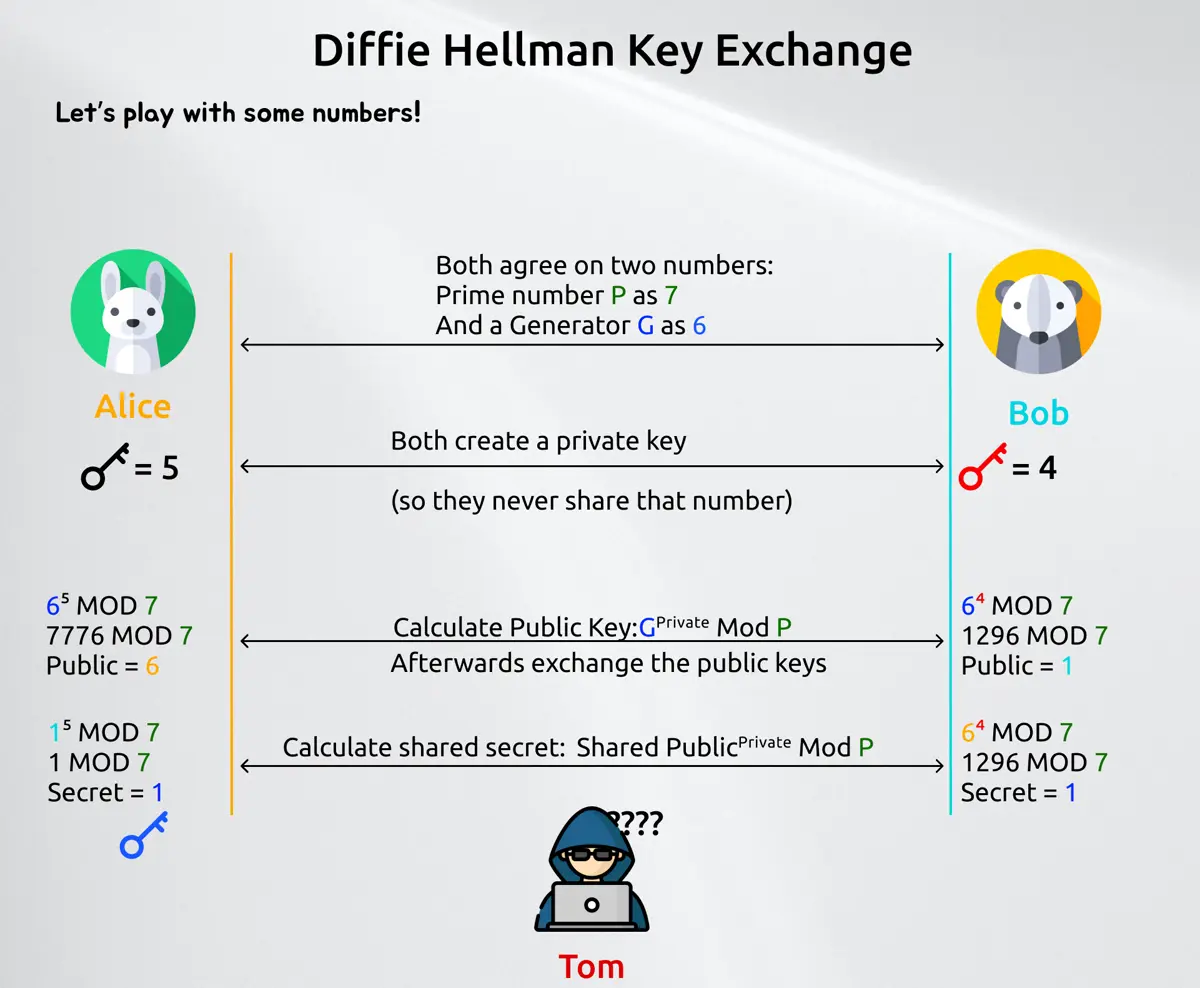
Now those numbers in the example are very small, so you can do trial and error until you can make sense of the message. In todays encryption (Stand 2022) we are dealing with prime numbers which are at least 22048 bit wide, so a number with over 600 digits.
The elegance why this works and why everyone can openly share the prime number plus the generator is simple: Discrete logarithm. As long as we can't solve that efficiently, we should be good for now.
Now we saw that this asymmetric key exchange is quite expensive and uses a few roundtrips to make it work. That is why that key is then only used to enable then symmetric encryption (now that we have a "secret channel"). So every other resource in the same domain and session is done via symmetric encryption (to be faster and more lightweight).