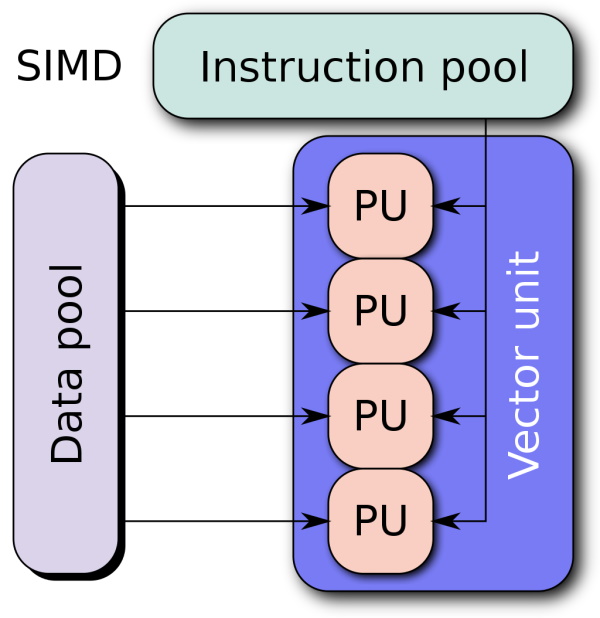
In this blog post, we will explore the use of SIMD instructions to speed up LINQ queries. We will use the Vector
The "problem"
Let's say we have a list of numbers and we want to find the sum of all the numbers. What would be the fastest way to do this? Well, we could use a for loop and add each number to a variable. But this is not the fastest way. The fastest way is to use SIMD instructions. SIMD stands for "Single Instruction Multiple Data". It allows us to perform the same operation on multiple data points at the same time. This is much faster than performing the same operation on each data point one by one. A word of warning: There are two pitfalls involved with this. 1. Complexity. Obviously, this approach is far more advanced than a simple loop or using LINQ directly. 2. I would not recommend this approach for small datasets and when performance is not critical. I said it before and I say it again: Measure your stuff first before you optimize at the wrong place!
Back to topic, let's see how we can do this.
The Vector<T> type
The entry point to SIMD operations is the Vector<T> type. It is a generic type that can hold a vector of data. The T type argument can be any numeric type. The Vector<T> type has a Count property that tells us how many elements it can hold. That is important because if we, for example, add two vectors which each other, we do this in "one" operation. The result will be a vector with the same number of elements as the input vectors. So the more elements we can hold, the faster our code will be. The size of how many elements your vector can hold depends on your architecture. Your CPU has something called SSE: "Streaming SIMD Extensions". This is a set of instructions that allow you to perform SIMD operations. The size of the vectors you can hold depends on the SSE version your CPU supports. For example, if your CPU supports SSE2, you can hold two elements in a vector. If your CPU supports SSE4.1, you can hold 4 elements in a vector. And so on. I wrote an article some time ago that also explains it to somewhat more detail: "Using SSE in C# on the example of the sum of a list".
Generic Math and SIMD
With the introduction of C# 10, we now have a new feature called "generic math". This allows us to use SIMD operations on any numeric type. This is great because we can now use SIMD operations on int, float, double, and so on without creating a function for each type. This is also great because we can now use SIMD operations on user-defined types. Let's see how this works.
Creating the Min function
For SIMD it is important that the data is as independent as possible. The idea is that we tile our problem into smaller subproblems those subproblems will be solved in a single operation. So if we have a vector of 4 elements, we want to perform the same operation on each element simultaneously.
In our case we have a Min function that should retrieve the smallest value in our array. To do so we tile the whole array into smaller chunks and check for each what is the smallest value.
public static T Min<T>(this Span<T> span)
where T : unmanaged, IMinMaxValue<T>, INumber<T>
For the sage of simplicity we use a Span<T>. The important part is we need contiguous memory as the memory blocks get streamed to your SIMD processor that can not handle arbitrary memory addresses. INumber<T> is a marker interface that tells us that the type is a number. IMinMaxValue<T> is a marker interface that tells us that the type has a minimum and maximum value. This is important because we need to initialize our result with the maximum value of the type. unmanaged is a constraint that tells us that the type is a value type and the type does not contain any reference type. This is important because we need to be able to store the type in a vector. Well, technically Vector<T> only has the constraint struct but as a struct can contain a reference type, we need to add the unmanaged constraint. So we can use stuff like stackalloc and prohibit scenarios where a struct with a reference type yields unexpected results.
The function itself is pretty simple. We first create a vector with the maximum value of the type. That is where the generic math really kicks in!
We also cast our Span directly to a Vector.
var spanAsVectors = MemoryMarshal.Cast<T, Vector<T>>(span);
Span<T> vector = stackalloc T[Vector<T>.Count];
vector.Fill(T.MaxValue);
var minVector = new Vector<T>(vector);
In this case we are using T.MaxValue because later we want to retrieve the minimum value. If we would use T.MinValue or T.Zero we are running into the problem that this might be the smallest value present and therefore would lead to wrong results. And by the way things like T.MinValue or T.Zero are possible because of generic math.
The next step is retrieving is comparing each vector entry against every other vector to retrieve the minimum:
foreach (var spanAsVector in spanAsVectors)
{
minVector = Vector.Min(spanAsVector, minVector);
}
In the end we will have a Vector with n-entries where one of them is the total minimum. BUt we are not done. MemoryMarshal.Cast<T, Vector<T>>(span); has a big downside: Assume our Vector<T>.Length is 4 and our input is a list with 9 entries. The function would only return 2 vectors. So all in all one element is missing. Therefore if we have a "left-over" we have to compare it against the vector we have so far. This is done by the following code:
var remainingElements = span.Length % Vector<T>.Count;
if (remainingElements > 0)
{
Span<T> lastVectorElements = stackalloc T[Vector<T>.Count];
lastVectorElements.Fill(T.MaxValue);
span[^remainingElements..].CopyTo(lastVectorElements);
minVector = Vector.Min(minVector, new Vector<T>(lastVectorElements));
}
Now the last part: We need to retrieve the minimum value from the vector.
var minValue = T.MaxValue;
for (var i = 0; i < Vector<T>.Count; i++)
{
minValue = T.Min(minValue, minVector[i]);
}
return minValue;
And there we go! We successfully implemented a SIMD version of the Min function. Let's see how this performs.
Performance
To measure the performance we will use the BenchmarkDotNet library. We will compare the performance of the SIMD version of the Min function with the performance of the non-SIMD (LINQ) version of the Min function. Here the setup code:
public class MinBenchmark
{
private readonly int[] _numbers = Enumerable.Range(0, 1000).ToArray();
[Benchmark(Baseline = true)]
public int LinqSum() => Enumerable.Min(_numbers);
[Benchmark]
public int LinqSIMDSum() => LinqSIMDExtensions.Min(_numbers);
}
And here are the results from my MacBook M1:
| Method | Mean | Error | StdDev | Ratio |
|------------ |---------:|--------:|--------:|------:|
| LinqMin | 166.9 ns | 0.94 ns | 0.78 ns | 1.00 |
| LinqSIMDMin | 125.3 ns | 0.69 ns | 0.61 ns | 0.75 |
Not bad! We are 25% faster than the LINQ version. Keep in mind that this is a very simple example.
More use cases - Average
Thanks to the generic math we can even do things like Sum or Average on user-defined types. I will link the whole library and code samples at the end of the blog post anyway. The Sum is almost like the Min method, therefore I will not show it here. A bit special might be Average though. Here is the code:
public static T Average<T>(this Span<T> span)
where T : unmanaged, INumberBase<T>, IDivisionOperators<T, T, T>
{
var length = T.CreateChecked(span.Length);
var divisionOperators = span.Sum() / length;
return divisionOperators;
}
Here are some key takeawys. We are using the IDivisionOperators<T, T, T> interface. This interface is a marker interface that tells us that the type has a division operator. So we are getting the generic sum and divide this by the amounts of entries in our list.
As the span.Length is a simple integer we have to convert it to the type of our list. This is done by the T.CreateChecked method. It takes any other number-like type and tries to convert it to our type in a checked fashion. This means that if the conversion would lead to an overflow, an exception is thrown. This is important because we do not want to silently ignore overflows. We are doing this because the / is only valid for the same type in generic math. So we can not divide an int by an int and get a double as result. That has a big pitfall here: If we are using just integers and we retrieve the average we will get an integer as result. So the Average of [1, 2] is 1.
Performance
Like before we are creating a benchmark and check the difference to the plain old LINQ method:
public class AverageBenchmark
{
private readonly float[] _numbers = Enumerable.Range(0, 1000).Select(f => (float)f).ToArray();
[Benchmark(Baseline = true)]
public float LinqAverage() => Enumerable.Average(_numbers);
[Benchmark]
public float LinqSIMDAverage() => LinqSIMDExtensions.Average(_numbers);
}
Results:
| Method | Mean | Error | StdDev | Ratio |
|---------------- |-----------:|--------:|--------:|------:|
| LinqAverage | 1,055.2 ns | 4.79 ns | 4.48 ns | 1.00 |
| LinqSIMDAverage | 179.9 ns | 1.00 ns | 0.94 ns | 0.17 |
Well. This is a huge difference. We are almost 6 times faster than the LINQ version.
Conclusion
With the introduction of generic math we can now do SIMD operations on user-defined types and for a wider range of types without adopting code. This is a huge step forward for the .NET ecosystem. Based on the examples I showed here, I created a small library called: LinqSIMDExtensions that also brings some more methods you can use besides Min and Average. In the readme you will also find the nuget package download.
Resources
- The source code as well as the library can be found here: LinqSIMDExtensions
- The nuget download can be found here: LinqSIMDExtensions